問題解決思考の基礎
問題解決は「すぐに解決策を考える」ことではない。本当に解くべき問題を見極め、構造的に分解し、仮説と検証のサイクルを回すことが本質である。
問題と課題の本質
問題（Problem）とは何か
問題とは「現状（As Is）」と「あるべき姿（To Be）」のギャップである。
このシンプルな定義が重要な理由は、問題を語るためには必ず「前提」が必要だということ。前提が異なれば、同じ現状でも問題の捉え方は変わる。
例：
- 前提A「売上は成長し続けるべき」→ 売上横ばいは問題
- 前提B「利益率を維持すべき」→ 売上横ばいは問題ではない可能性
前提を定義する
問題を定義する前に、「変えられないこと」を明確にする必要がある。前提が曖昧なまま問題解決を進めると、途中で「そもそもそれは変えられない」と判明して手戻りが発生する。
前提の明示化
- 前提を洗い出す - 暗黙の前提を言語化する。「当然こうだろう」と思っていることを列挙
- 変えられるか確認する - 本当に変えられないのか、それとも変えないと決めただけなのか検証
現状の整理
同じ現状でも、何を制約として扱うかで課題の定義は全く変わる。
例えば「チームの残業が多い」という現状に対して：
- 「人員は増やせない」を制約とすると → 課題：業務効率化
- 「業務量は減らせない」を制約とすると → 課題：人員増加
- 「納期は変えられない」を制約とすると → 課題：スコープ削減
ここで重要なのは、「人員は増やせない」などは本当の制約（物理的・法的に不可能）ではなく、前提（変えないと決めたこと）である可能性が高いということ。前提を問い直すことで、より良い解が見つかることもある。ただし、前提を変えるには通常、より上位の意思決定者やステークホルダーとの交渉が必要になる。
前提と制約の違い
| 制約 | 前提 | |
|---|---|---|
| 定義 | 物理的・法的に変えられない | 変えられるが、変えないと決めた |
| 例 | 法律、物理法則、契約 | 予算、スコープ、方針、納期 |
| 扱い | 受け入れる | 問い直す余地がある |
ここでは、前提と制約を上記の定義として扱う。前提を制約と混同すると、本来は変えられる選択肢を見落とす。「それは本当に変えられないのか？」と問い直すことが、真の課題を見極める第一歩になる。
Problem と Issue の違い
英語では problem と issue を区別する。この区別が問題解決の質を変える。
| Problem | Issue | |
|---|---|---|
| 焦点 | 望ましくない状態・ギャップ | 決めるべき論点・争点 |
| 性質 | 「何かがおかしい」 | 「どうするか決まっていない」 |
| 行動 | 解決すべき | 意思決定すべき |
イシューとは「答えを出す価値のある本質的な問い」。問題解決の鍵は、漠然とした problem から具体的な issue を抽出することにある。
問題解決のプロセス
全体像
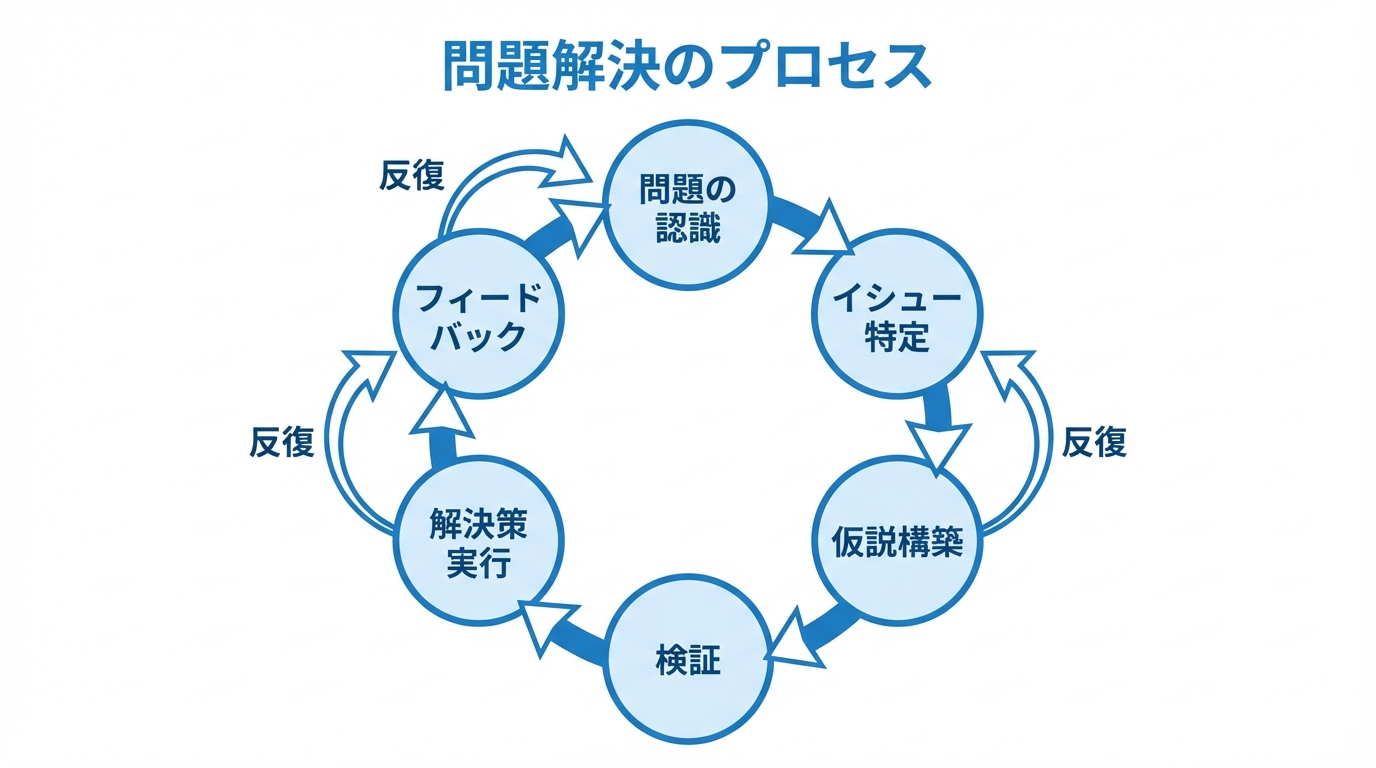問題の認識からフィードバックまで、各ステップを反復しながら進める
このプロセスは直線的ではなく、フィードバックループを持つ。検証結果によって仮説を修正し、ときには問題の認識自体を見直す。
イシュードリブンなアプローチ
イシュードリブンとは、「何を解くか」を最初に見極めるアプローチ。
100の問題があっても、本当に答えを出すべき問題は2〜3個。残り97〜98個に時間を使うのは犬の道であり、バリューのある仕事は生まれない。
よいイシューの条件：
- 本質的な選択肢である - 答えによって意味合いが大きく変わる
- 深い仮説がある - 常識を覆す、新しい構造で説明するなど
- 答えを出せる - 手持ちの技術・手法で検証可能
論理的思考の構造
問題解決には論理的思考が不可欠である。しかし「論理的」とは何を意味するのか。
論理的ではない思考
以下のような思考は、一見もっともらしく見えても論理的ではない：
- 「若者のユーザーは、…といっている」
- 「売上の伸びが鈍化…」
- 「業界のエキスパートは、…といっている」
- 「過去のベストプラクティスは…」
- 「最近の競合の動きは、…」
これらは情報を羅列しているだけで、情報の関連性・重要性が明確ではない。事実やデータを並べることと、論理的に考えることは別物である。
論理的とは何か
論理的であるとは、「話が縦にも横にもきちんとつながっている」ことである。
| 方向 | 意味 | チェックポイント |
|---|---|---|
| 縦の論理 | 因果関係が整理されている | 「本当にそうなの？」（話が飛んでいないか） |
| 横の論理 | 全体が網羅されており抜け漏れ重複がない | 「本当にそれだけ？」（抜けていないか） |
縦の論理と横の論理の両方が満たされれば、人は誤解や違和感なく理解できる。
縦の論理
縦の論理を構成する方法は2つある。帰納法と演繹法である。
| 方法 | 定義 | 特徴 |
|---|---|---|
| 帰納法 | 具体的な例を挙げて共通項を導く | 複数事例からパターンを発見 |
| 演繹法 | 前提を積み重ねて必然的に導く | 前提が正しければ結論も正しい |
具体例：子供が親に靴を買ってもらうとき
帰納法の例：
- A君は新しい靴を買ってもらった
- B君も新しい靴を買ってもらった
- C君も新しい靴を買ってもらった
- → だから僕にも新しい靴を買ってほしい
演繹法の例：
- 徒競走で優勝したい
- 今の靴では走りにくい
- 優勝するためには新しい靴が必要
- → だから僕に新しい靴を買ってほしい
どちらも「新しい靴を買ってほしい」という結論に至るが、説得の構造が異なる。帰納法は「みんなが持っている」という事実の集積、演繹法は「目標達成に必要」という論理の連鎖で支える。
Why So? と So What?
縦の論理を検証する2つの問いがある。
| 問い | 方向 | 意味 |
|---|---|---|
| Why So? | 上→下 | 「なぜそう言えるのか？」メッセージを根拠で支える |
| So What? | 下→上 | 「だから何？」得られた情報から言えそうなことを抽出する |
ビジネスでの具体例：
主張：「ベトナムのB社を委託生産先および市場進出の第一候補とすべき」
- Why So? → B社の生産コストが一番安い
- Why So? → 委託リスクは中国以外は十分低い
- Why So? → 市場魅力はベトナムが一番高い
「帰納法」か「演繹法」で、メッセージを根拠で支えるのが縦の論理の基本である。
横の論理
大きな問題をそのまま解くことはできない。答えを出せるサイズまで分解する技術が必要。横の論理を構成するのはMECEとGroupingである。
MECE（Mutually Exclusive, Collectively Exhaustive）
「漏れなく、ダブりなく」分解する原則。考えるポイントを抜け漏れダブりなく分解することで、横の論理を担保する。
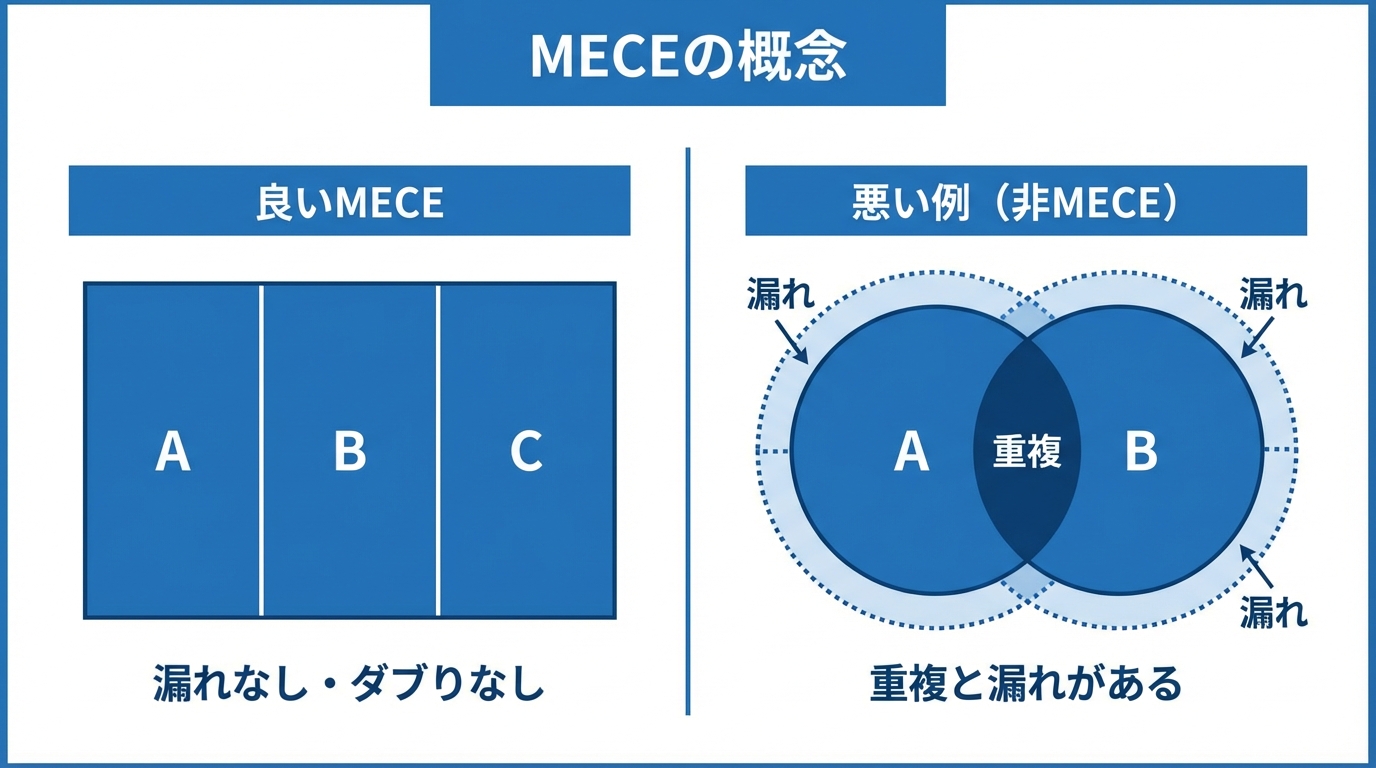左：Good MECE（重なりなし、隙間なし）、右：Bad（重複と隙間あり）
MECEの4つの作り方
| 方法 | 説明 | 例 |
|---|---|---|
| 二分割（A−Not A） | 対立概念で二分する | 国内/海外、新規/既存、大企業/中小企業 |
| プロセス分割 | 時間・手順の流れで分ける | 訪問→商談→見積→契約 |
| 数式分割 | 数式の構成要素で分ける | 売上 = 市場規模 × シェア |
| フレームワーク分割 | 既存の枠組みを使う | PEST、3C、4Pなど |
数式分割の例：
| 分解式 |
|---|
| 売上 = 社員数 × 社員一人当たり売上 |
| 売上 = 市場規模 × シェア |
| 売上 = A事業部売上 + B事業部売上 + C事業部売上 |
Grouping
要素をグルーピングして意味ある順序にまとめることで、横の論理を担保する。
Groupingの3つの根拠
| グルーピング方法 | 説明 | 並べ方 |
|---|---|---|
| 因果の因 | 果の根拠となる因でまとめる | 時間の順序（プロセス順） |
| 部分/全体の部分 | 全体を構成する部分でまとめる | 構造の順序（上流→下流など） |
| 類似するもの | 意味・形状・性質などでまとめる | 度合いの順序（重要度、規模など） |
ロジックツリー
問題を木構造で分解する手法。分解の切り口によって複数の型がある。
- Where型（どこに問題があるか） - 製品別、地域別などで問題の所在を特定
- What型（何が問題か） - 問題の要素を分解して特定
- Why型（なぜ問題が起きているか） - 因果関係を掘り下げて根本原因を特定
- How型（どうやって解決するか） - 解決策の選択肢を構造化
分解の視点
同じ問題でも、切り口によって見える世界が変わる。複数の切り口を試すことで、問題の本質に迫れる。
| 切り口 | 例 |
|---|---|
| プロセス | 調達→製造→販売→アフターサービス |
| 顧客セグメント | 法人/個人、業種別、規模別 |
| 時間軸 | 過去→現在→未来 |
| 地理 | 地域別、国別 |
| 製品/サービス | カテゴリ別、SKU別 |
| 4P/4C | Product, Price, Place, Promotion |
ピラミッド構造
論理的な思考や説明は「ピラミッド構造」で表現できる。ピラミッド構造では、縦と横の論理が共に適切である必要がある。
| 方向 | 構成要素 | 役割 |
|---|---|---|
| 縦の論理 | Why So? / So What? | メッセージを根拠で支える / 情報から意味を抽出する |
| 横の論理 | MECE / Grouping | 抜け漏れダブりなく分解 / 意味ある順序で並べる |
具体と抽象の往復
問題解決では、観察の粒度を意識的に切り替える必要がある。
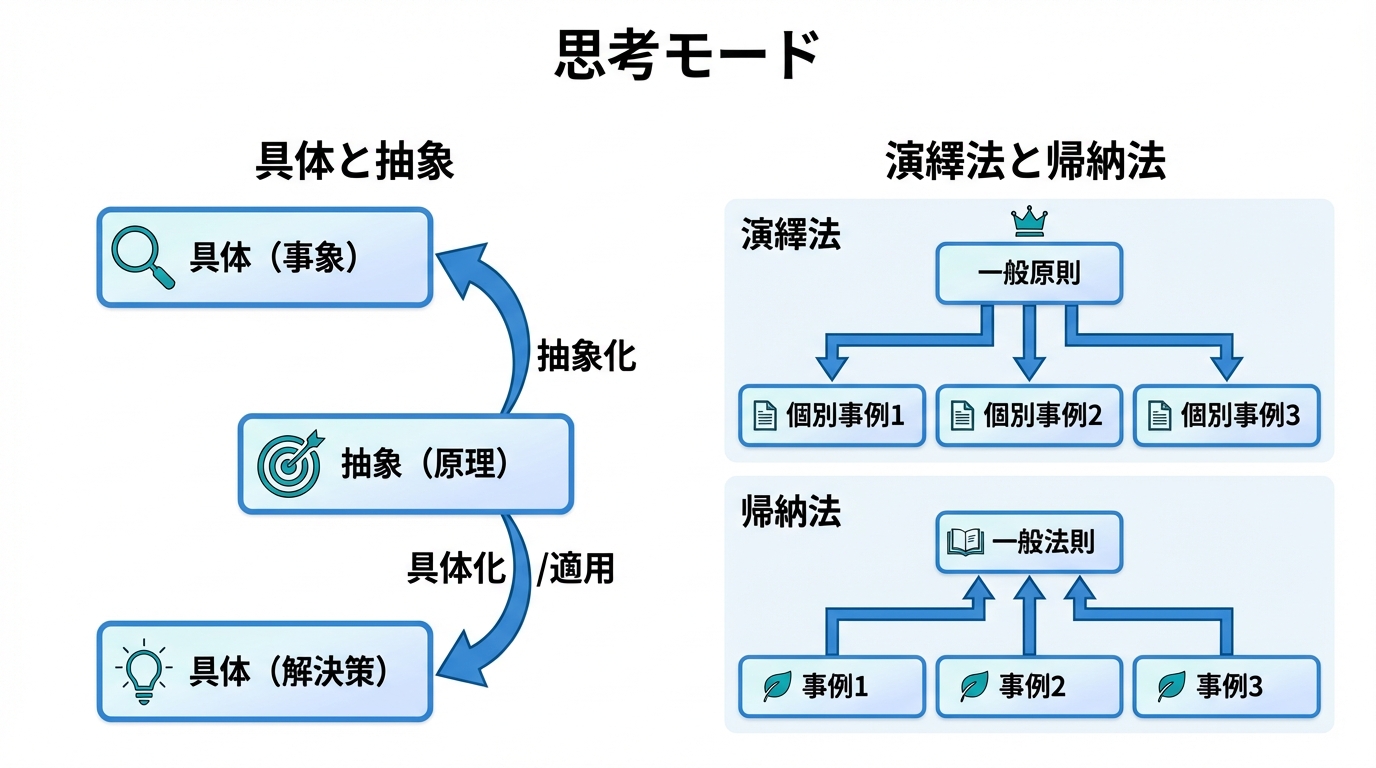具体と抽象の往復（事象→原理→解決策）
観察の粒度としての具体⇔抽象
| 思考の方向 | 特徴 | 使いどころ |
|---|---|---|
| 具体化 | 詳細に落とし込む、事例を挙げる | 検証フェーズ、実行計画 |
| 抽象化 | 本質を抽出、共通項を見出す | 問題の構造化、パターン認識 |
問題解決では具体と抽象化を往復する。具体的な事象から抽象的な構造を見出し、その構造を別の具体的な状況に適用する。
仮説生成のプロセス
「システムが遅くなった」という観察から「データベースのクエリが原因ではないか」という仮説を立てる。この仮説生成は、しばしばアブダクション（仮説的推論）と呼ばれ、演繹・帰納と並ぶ「第三の推論形式」として紹介されることが多い。
しかし、アブダクションを演繹・帰納と同列に扱うことには問題がある。
アブダクションの形式的構造：
もし H ならば E が起きる
E が観察された
∴ H である
これは論理学では「後件肯定の誤謬」と呼ばれる形式であり、妥当な推論ではない。
仮説生成の実際のプロセス：
実際に仮説を「思いつく」過程を観察すると、複数の要素が組み合わさっている：
- 帰納的要素 - 「前にも似たような遅延があり、そのときはDBが原因だった」という過去の事例からのパターン認識
- 演繹的要素 - 「クエリが重いとレスポンスが遅くなる」という既知の原理の適用
- 問いの設定 - 「何が説明変数になりうるか」という視点の選択
つまり仮説生成は、帰納・演繹・問いの設定の複合プロセスである。「アブダクション」という名前は、この複合プロセスの結果（仮説が生まれること）に名前を付けたものである。
仮説思考で重要なのは、この複合プロセスを意識的に回すこと。そして生成された仮説は必ず検証が必要である。
フェーズごとの思考の対応
| フェーズ | 主な思考 |
|---|---|
| 問題認識 | 抽象化、前提の問い直し |
| イシュー特定 | 具体化、前提の問い直し |
| 課題分解 | 抽象化、演繹（MECE適用） |
| 仮説構築 | 帰納（パターン認識）、演繹（原理適用）、問いの設定 |
| 検証 | 演繹、具体化 |
| フィードバック | 帰納、前提の問い直し |
前提を問い直す思考
問題解決において、帰納・演繹は「縦の論理」を構成する推論形式である。一方、「前提を問い直す」という行為は、推論形式とは異なる次元の思考である。
メタ認知とは
自分の思考を客観視する認知。「なぜ自分はこの問題を問題と捉えているのか」を問う。
| レベル | 思考内容 |
|---|---|
| 通常の認知 | この問題を解こう |
| メタ認知 | なぜこれを問題と捉えているのか？前提は正しいか？ |
前提を問い直す4つの場面
メタ認知が特に重要になる場面は4つある。
1. 問題定義時：前提の明示化
問題を定義する際に、暗黙の前提を言語化する。前提が曖昧なまま進めると手戻りが発生する。
- 「変えられないこと」を洗い出す
- 「変えられるが変えないと決めたこと」を区別する
2. 仮説生成時：問いの設定
仮説を生成する際に、「何を説明変数として考えるか」という問いを設定する。この問いの設定自体がメタ認知である。
- 「この現象を説明する要因として何が考えられるか？」
- 「過去の類似事例では何が原因だったか？」
- 「どの切り口で分析するのが効果的か？」
3. 分析を通じた前提の洗練
分析を進める中で、前提の解像度が上がることがある。最初は曖昧だった前提が、具体的なデータや事例に触れることで精緻化される。
前提の洗練パターン：
| パターン | 例 |
|---|---|
| 適用範囲の限定 | 「顧客は価格に敏感」→「新規顧客は価格に敏感だが、既存顧客はサービス品質を重視」 |
| 定義の精緻化 | 「生産性が低い」→「定型業務の処理速度は問題ないが、非定型業務の着手が遅い」 |
| 条件の発見 | 「このシステムは遅い」→「データ量が閾値を超えると急激に遅くなる」 |
このフィードバックループを回すことで、最初に設定した課題が変わることは珍しくない。むしろ、課題設定が変わらないまま分析が進むときこそ、前提を問い直すべきサインかもしれない。
4. 行き詰まり時：真の課題の発見
問題解決が行き詰まったとき、前提自体を問い直すことで突破口が見つかる。
- 「そもそもこの問題設定は正しいか？」
- 「別の前提を置いたらどうなるか？」
- 「制約だと思っていたものは本当に変えられないのか？」
シングルループとダブルループ
ダブルループ学習の概念は、前提を問い直す思考を理解する上で重要。
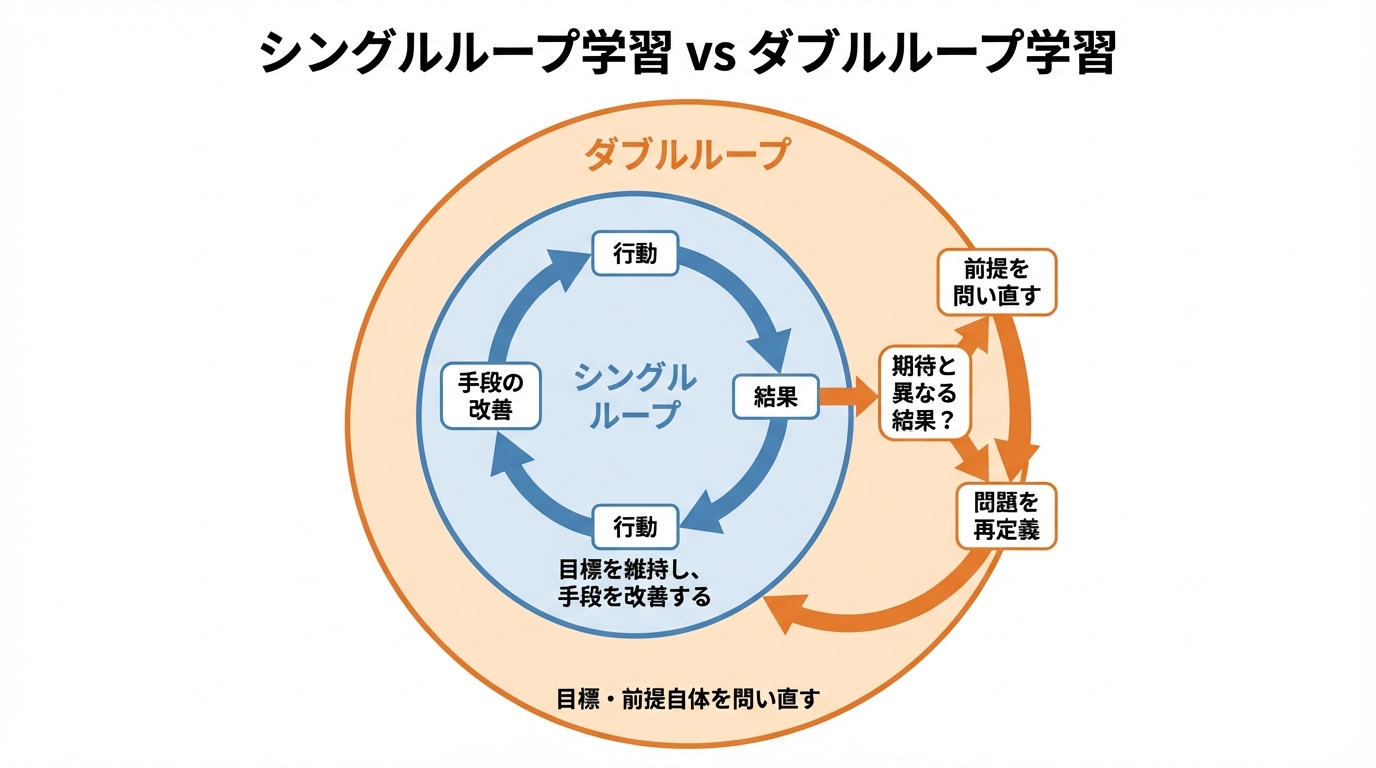青の内側ループ：手段の改善に留まるシングルループ、オレンジの外側ループ：前提自体を問い直すダブルループ
| ループ | 焦点 | 問い |
|---|---|---|
| シングルループ | 手段の改善 | 「どうやって目標を達成するか？」 |
| ダブルループ | 前提の見直し | 「その目標は正しいか？前提は妥当か？」 |
表面的な問題に囚われている状態は、シングルループに閉じ込められている状態。メタ認知でダブルループに移行することで、真の課題に到達できる。
真の課題を見極める
表面的な問題から深層へ
最初に認識される問題は、往々にして「表面的」である。
例えば「チームの生産性が低い」という表面的な問題に対して「なぜ？」を繰り返すと、「メンバーのスキルが足りない」→「採用基準が曖昧で、評価とフィードバックの仕組みがない」という真の課題に到達する。
表面的な問題に対する解決策（研修を増やす）は対症療法に過ぎない。真の課題（採用・評価の仕組み）に取り組まなければ、問題は繰り返される。
分析から課題を抽出する
真の課題を見極めるとは、縦と横の論理で分析した結果から「問題に効果的にアプローチできる課題」を抽出することである。
横の論理：問題の構造を把握する
MECEで問題を分解し、どこに問題があるかを特定する。
| 分解の切り口 | 問い |
|---|---|
| プロセス | どの工程で問題が発生しているか？ |
| リソース | 人・モノ・金・時間のどこに制約があるか？ |
| 構成要素 | どの部分・機能に問題があるか？ |
縦の論理：因果関係を追求する
Why So?で因果を掘り下げ、根本的な説明変数を特定する。
| 深掘りの観点 | 問い |
|---|---|
| スキル | 必要な能力と現状のギャップは？ |
| 仕組み | ルール・制度・システムに問題はないか？ |
| インセンティブ | 望ましい行動を促す構造になっているか？ |
課題候補の評価
分析で特定した説明変数から課題候補を導出し、So What?で意味合いを抽出する。
| 評価軸 | 問い |
|---|---|
| 効果 | この課題を解いたら、問題はどの程度解決するか？ |
| 持続性 | 一時的な改善か、恒久的な解決か？ |
| 実現性 | 現在の前提・制約の下で実行可能か？ |
| 副作用 | 解決によって新たな問題が生じないか？ |
課題のレベル感
課題には「対症療法」から「構造改革」までレベルがある。どのレベルで介入すべきかを見極める必要がある。
| レベル | 介入対象 | 例 | 効果の持続性 |
|---|---|---|---|
| 対症療法 | 症状 | エラーが出たら手動で修正 | 低（再発する） |
| オペレーション改善 | 作業方法 | チェックリストを導入 | 中（人に依存） |
| 仕組み改善 | ルール・制度 | 承認フローを変更 | 高（仕組みで担保） |
| 構造改革 | 組織・システム | 部門再編、システム刷新 | 最高（根本解決） |
レベル選択の判断軸
- 同じ問題が繰り返されている → より上位レベルでの介入を検討
- 複数の部門・プロセスにまたがる → 仕組み改善または構造改革
- インセンティブ構造が問題 → 構造改革が必要な可能性
- リソース制約が厳しい → 実現可能なレベルから着手
構造改革は効果が高いがコストとリスクも大きい。「最小の介入で最大の効果」を狙うなら、まず仕組み改善で対応できないかを検討し、それでも不十分な場合に構造改革を選択する。
問い直しの技法
真の課題に到達するには、メタ認知を実践する。具体的な問い直しの技法は以下の通り。
- 前提を疑う：「本当にそれは問題か？」
- 視点を変える：「別の立場から見たらどうか？」
- 時間軸を変える：「1年後、5年後にも問題か？」
- スケールを変える：「これは部分の問題か、全体の問題か？」
これらの問いを通じて、シングルループ（手段の改善）からダブルループ（前提の見直し）に移行し、真の課題に到達できる。
「解くべきでない問題」を見極める
すべての問題を解く必要はない。以下の問いで、本当に取り組むべきかを判断する：
- 今、答えを出す必要があるか？（タイミング）
- 答えが出たとして、行動が変わるか？（アクショナブル）
- 自分（たち）が解くべき問題か？（当事者性）
- 解くためのリソースがあるか？（実現可能性）
説得力をもって伝える
問題を解くだけでは不十分である。分析結果を他者に伝え、理解を得て、行動を促すまでが問題解決のプロセスである。
なぜ「伝える」が問題解決の一部なのか
どれほど優れた分析をしても、意思決定者や実行者に伝わらなければ問題は解決しない。「伝える」は問題解決の最終ステップではなく、解決の一部である。
伝えることの目的は3つある：
| 目的 | 内容 |
|---|---|
| 認識の共有 | 問題の存在と本質を相手に認識させる |
| 納得の獲得 | なぜその課題に取り組むべきか、なぜその解決策なのかを納得させる |
| 行動の促進 | 具体的な行動を起こさせる |
この3つが揃って初めて、問題解決は完結する。
前提の共有から始める
説明の最初にすべきことは、具体的な分析結果や提案を示すことではない。まず「何が問題なのか」という認識を相手と共有することである。
As-Is / To-Be の共有
問題とは「現状（As Is）と あるべき姿（To Be）のギャップ」である。このギャップの認識が相手と揃っていなければ、どれほど論理的な説明も空回りする。
共有すべき3つの要素：
- 現状（As Is）の認識 - 「今、何が起きているか」の事実認識は揃っているか
- あるべき姿（To Be）の認識 - 「どうあるべきか」の目標認識は揃っているか
- ギャップの大きさ - そのギャップは対処すべき問題なのか、許容範囲なのか
特に「あるべき姿」は、立場や価値観によって異なる。自分にとっては明らかな問題でも、相手にとっては問題ですらないことがある。まずここを揃える。
相手のコンテキストを把握する
相手が持っている前提知識、関心事、制約を把握した上で説明を組み立てる。
| 把握すべき項目 | 問い |
|---|---|
| 知識レベル | 専門用語は通じるか？背景知識はあるか？ |
| 関心事 | 相手は何を気にしているか？何を知りたいか？ |
| 立場・制約 | 相手の意思決定に影響する制約は何か？ |
| 過去の経緯 | この問題について相手はどんな認識を持っているか？ |
相手のコンテキストを無視した説明は、どれほど論理的でも響かない。「正しいこと」と「伝わること」は別である。
重要な前提は具体的説明の前に
分析結果や提案を示す前に、理解に必要な前提知識を共有する。相手が知らない概念や用語を使って説明を始めると、内容以前に「何を言っているかわからない」状態になる。
前提共有のポイント：
- 専門用語を使う場合は、最初に定義を明示する
- 分析に使った枠組み（MECEの切り口、ロジックツリーの構造など）を先に説明する
- 「なぜその切り口で分析したか」の理由も添える
分析結果を構造的に伝える
縦の論理と横の論理で構築した分析は、その構造を活かして伝える。
横の論理：どう分解したかを示す
MECEで分解した構造を示し、「全体のどこに問題があるか」を明確にする。
伝えるべきは結果だけでなく、「どういう切り口で分解したか」「なぜその切り口を選んだか」である。これにより、分析の網羅性と妥当性を示せる。
| 伝える要素 | 内容 |
|---|---|
| 分解の切り口 | どのような軸で問題を分解したか |
| 切り口の選定理由 | なぜその切り口が適切なのか |
| 問題の所在 | 分解の結果、どこに問題が特定されたか |
縦の論理：なぜそう言えるかを示す
Why So? で掘り下げた因果関係を示し、「なぜその結論に至ったか」を明確にする。因果の連鎖を示すことで、「話が飛んでいない」ことを相手に確認させる。
課題抽出の根拠を示す
分析から課題を抽出する際の So What?（だから何が言えるか）を明示する。課題候補を示した上で、なぜその課題を選定したかの評価軸（効果、実現性、持続性など）も併せて説明する。
ストーリーラインの構築
分析結果を伝える全体の流れがストーリーラインである。代表的な構成パターンを使い分ける。
空・雨・傘
事実→解釈→行動の流れで構成する。問題認識から行動提案までを一貫した論理で繋ぐ。
空（事実）：西日本の主要顧客3社が競合B社に切り替えた
↓
雨（解釈）：価格競争力の低下が原因。放置すれば他地域にも波及する
↓
傘（行動）：コスト構造を見直し、3ヶ月以内に価格改定を実施すべき
この構造が崩れると説得力が失われる：
| 崩れ方 | 問題 |
|---|---|
| 空なき雨 | 事実の裏付けがない解釈（思い込み） |
| 雨なき傘 | 解釈を飛ばした行動提案（唐突） |
| 傘なき雨 | 解釈だけで行動提案がない（だから何？） |
Whyの並び立て
結論を複数の根拠で支える構成。ピラミッド構造の横の論理を活かす。
主張：コスト構造の見直しを優先すべき
なぜなら：
├── 1. 価格差が競合切り替えの主因である（効果が高い）
├── 2. 製造工程の見直しで15%のコスト削減が見込める（実現可能）
└── 3. 他の施策より短期間で効果が出る（即効性）
論理と感情のバランス
説得には論理だけでなく感情への働きかけも必要である。
| 要素 | 役割 | 手法 |
|---|---|---|
| ロゴス（論理） | 納得させる | データ、因果関係、構造化された説明 |
| パトス（感情） | 共感させる | 具体的なエピソード、危機感、将来像 |
| エトス（信頼） | 信じさせる | 実績、専門性、誠実な姿勢 |
論理だけでは人は動かない。感情だけでは持続しない。信頼がなければそもそも聞いてもらえない。3つのバランスを意識する。
感情に働きかける具体例：
- 抽象的な数字だけでなく、具体的な顧客の声を紹介する
- 「このまま放置すると何が起きるか」の危機シナリオを示す
- 「解決した後の姿」をビジョンとして描く
伝える際のチェックリスト
| 観点 | チェック項目 |
|---|---|
| 前提共有 | As-Is / To-Be の認識は相手と揃っているか？ |
| 前提共有 | 相手のコンテキスト（知識、関心、制約）を把握しているか？ |
| 前提共有 | 必要な前提知識を具体的説明の前に共有したか？ |
| 構造 | 分解の切り口とその理由を説明したか？ |
| 構造 | 因果関係の各ステップは飛躍がないか？ |
| 構造 | So What?（だから何が言えるか）に答えているか？ |
| 行動 | 具体的に何をすべきかが明確か？ |
| 行動 | 想定される反論に先回りして対処しているか？ |
| 表現 | 1チャート1メッセージになっているか？ |
| 表現 | 論理だけでなく感情にも働きかけているか？ |
まとめ：問題解決の心構え
- すぐに解決策を考えない - 表面的な問題に飛びつかず、真の課題を見極める
- イシューから始める - 何を解くかを最初に決める。犬の道を避ける
- 論理的に考える - 縦の論理（因果関係）と横の論理（網羅性）の両方を満たす。ピラミッド構造で思考を整理する
- 具体と抽象を往復する - 事象から構造を見出し、構造を別の状況に適用する
- 前提を問い直す - 問題定義時、仮説生成時、行き詰まり時にメタ認知を働かせる
- 分解して扱えるサイズにする - MECE・Groupingで横の論理を、Why So?・So What?で縦の論理を担保する
- 仮説→検証のサイクルを回す - 仮説なき分析は単なる作業
- 伝えるまでが問題解決 - ストーリーライン、論理と感情のバランス
問題解決は技術であり、意識的な訓練で向上する。まず「解く」前に「見極める」ことから始めよう。